What is Big O Notation ? Why do we need it ?
TL;DR
Big O is the objective way to measure the code we write. We can use this to determine which code suits the problem better
In problem solving, there are many possible way we can solve a simple problem: for example:
Option 1-
const multiplyNumber = (num1, num2, num3) => {
return num1*num2*num3
}
or Option 2-
const multiplyNumber = (num1, num2, num3) => {
let sum = 0
sum = num1 *num2
sum = sum * num3
}
How do we decide which one of the solutions is better? By using the concept of Big O. There are 2 main types of Big O complexity, they are:
Big O - Time Complexity
Can we use the time required to complete an algortihm as a measure? Nope. Why?
- Different machines take different times to execute a piece of code.
- Same machines, take different time to execute a piece of code.
- Very fast algorithms, cannot be differentiated by time.
- Time cannot be the only constraint that we should think about, there is the factor of memory that is available.
What's the alternative that can be used? Count the number of simple operations that are in each program. The general rule of thumb is the number of simple operations will increase as the number of times the function is called.
For example, here as the 'number' increases the number of simple operations increase.
const addNumbers = (number) => {
let sum = 0
let i = 1
// looping from i = 1 to number
while(i <= number) {
sum += i
i++
}
return sum
}
In a way, Big O can be said as a relationship between input size and the time required to complete the program relative to the input size.
Different types of Big O time complexity:
- O(1) - Constant time: If an algorithm has an O(1), its time complexity will stay constant, no matter the value of n. This is the best possible outcome for any algorithm.
O (log n) - Quadratic time: An algorithm with an O(log n) rises in time complexity with n, but eventually levels off.
O(n)- Linear time: If an algorithm has an O(n), as ’n’ increases, so does the amount of operations needed to complete the problem.
O(n log n) - Quadratic time: If an algorithm has O (n log n) rises in time complexity with n, this takes the second most amount of time, after O (n^2) to complete the algorithm.
O(n^2) - Quadratic time: An algorithm with an O(n ²) increases exponentially with n. This takes the most time to complete the algorithm.
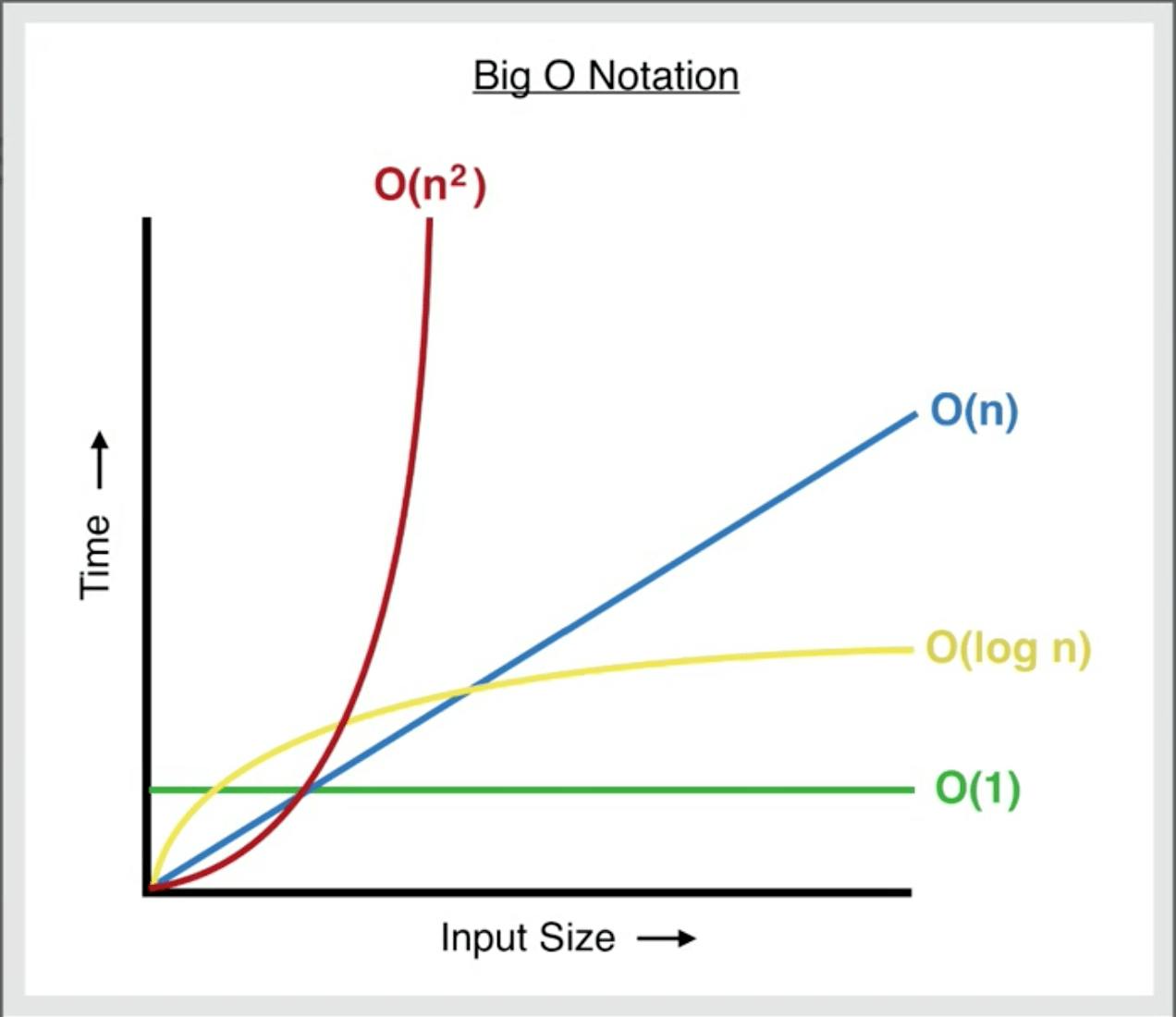 Pic Courtesy: levelup.gitconnected.com/big-o-time-complex..
Pic Courtesy: levelup.gitconnected.com/big-o-time-complex..
P.s: Big O always describes the worst case scenario.
Big O - Space Complexity
Can be simplified as how many different variables are getting initialised and what amount of space is needed to store these particular variables.
Disclaimer: I am using the blog as a digital notebook, where I can comeback and take a peak at if I am stuck anytime. I highly recommend that you take the full course available on Udemy: udemy.com/course/js-algorithms-and-data-str..
Other sources:

